Integración en el plano complejo
- Las definiciones de integrales en el campo complejo son similares a las integrales de funciones reales de 2 variables
- Se aplican las reglas y propiedades de integración de las funciones de variable real, salvo el caso en que las funciones carezcan de anti-derivada
- Los números reales se representan en una recta como intervalos, entonces tiene sentido las sumas de Riemann
- Los números complejos se representan en el plano complejo, lo cual nos lleva a considerar las integrales de linea, sobre una curva r en lugar de las sumas de Riemann
- En las integrales cerradas se presentan novedades tales como las integrales de Cauchy, que son propios de los números complejos
- Integración Indefinida
- Integrales de Linea
- Curvas en el plano complejo
* La curva r en el plano complejo, es el conjunto de puntos (x,y) tales que:

La curva r se representa en forma paramétrica :

donde a < t < b
Curva suave
Una curva que no presenta entrecruzamiento o puntos dobles se llama curva suave o curva simple
-PROPIEDADES
Si r es una curva suave o suave por intervalos y f(z) es continua entonces:

(-r) denota la curva r en sentido negativo de mas o menos
- Si r es una curva suave y se representa por Z(t) = x(t) + iy(t) para a<t<b y f(z) continua en c entonces:
- Integrales Cerradas
- Las integrales cerradas se evaluan de igual forma que las integrales de linea, la unica diferencia es que la curva r debe ser una curva cerrada.
i) f: es analitica
ii) D: simplemente conexo
iii)C : curva cerrada simple
Teorema de la Deformación

Dominio Simplemente Conexo
Teorema de la Integral de Cauchy
-Sea f(z) una función analítica en D, un dominio conexo y sea C una curva cerrada simple en D entonces:
ii) D: simplemente conexo
iii)C : curva cerrada simple
Teorema de la Deformación
Sea f(z) analítica en D, excepto en Zo y sean C y S curvas cerradas simples que encierran a zo, entonces:


Si f es analítica en un
dominio D simplemente conexo. Sea la curva cualquier curva cerrada en D, que
encierre a Zo

Si f es analítica en un
dominio D simplemente conexo. Sea la curva cualquier curva cerrada simple en D,
que encierra a Zo

- Sucesiones y Series de variable compleja
SUCESIONES
- Las sucesiones y series de variable compleja son similares a las de variable real. Para determinar su convergencia se utilizan los criterios de convergencia de sucesiones y series reales.
- La serie de Laurent es propia de los números complejos y es una generalización de la serie de Taylor
Definición:






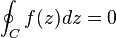















No hay comentarios:
Publicar un comentario