Octubre



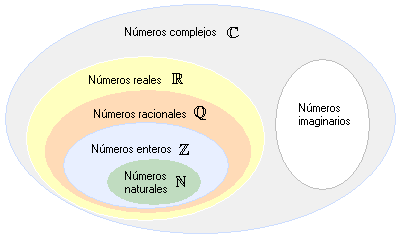
Los Números Complejos




  • Todo numero real es un número complejo
  • No todo numero complejo es un número real
Represetanción algebraica o binómico de un numero complejo

Z= X + iY

Donde: 
X es la parte real 
Y es la parte imaginaria

Representación cartesiana




Propiedad de igualdad entre números complejos

Si Z1= X1 + iY1    y Z2= X2 + iY2  entonces Z1= Z2 <-----> X1 = X2   y Y1 = Y2  (se puede usar de izquierda a derecha o viceversa)

* Casos Particulares
  1. Si Re(Z)=0  y Im(Z)=0 entonces Z=0 + 0i    Z = 0 Cero complejo
  2. Si Re(Z)=0  y Im(Z) diferente de 0 entonces Z=0 + Yi    Z = Yi Imaginario Puro
  3. Si Re(Z) diferente de 0  y Im(Z) = 0 entonces Z=0 + Yi    Z= X+0i Número Real

Operaciones con números complejos

Para sumar dos números complejos sumamos las dos partes por separado:
(a,b) + (c,d) = (a+c, b+d)
Ejemplo: (5 + i) + (3 + 9i) = (8 + 10i)

Los numeros complejos cumplen con la propiedad Clausurativa, Conmutativa y Asociativa


Elemento Neutro:
Z = 0 + 0i        Cero Complejo

Elemento opuesto:
-Z = -X - Yi

 Producto:

 Para realizar la multiplicación :
(a,b)(c,d) = (ac-bd, ad+bc)
Ejemplo: (2 + 5i)(3 + 4i) = ((2×3 - 5×4) + (2×4 + 5×3)i) = -14 + 23i

tomando en cuenta :



Cumple con la propiedad:
- Clausurativa
- Conmutativa
- Asociativa 
- Distributiva

 Neutro Multiplicativo:
Z = 1 + 0i
Conjugado de Z:


Inverso Multiplicativo:




Propiedades de Z

Algunas propiedades que faltan por indicar son:



División Caso particular del producto

 Dado Z1=a+ib  y  Z2=c+id, entonces Z1 / Z2 = 



También se puede realizar de la siguiente forma:
Z1/Z2 = Z1*Z2' 
donde Z2' es la conjugada de Z2

 Representación Polar
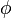\textstyle{\phi} = \arctan \left(\frac{b}{a}\right) = \arctan \left( \frac{\hbox{Im}(z)}{\hbox{Re}(z)}\right) = -\arctan \left ( -\frac{\hbox{Im}(z)}{\hbox{Re}(z)}\right)
Donde \textstyle{r} es el módulo del número complejo 
\textstyle{\phi} es el argumento del número complejo.

\cos \phi = \frac{a}{r} \ , \ \sin \phi = \frac{b}{r}

Representación Binomial:
                                         z = a + \mathrm{i}b ;\; z = r\cos{\phi} + \mathrm{i}r\sin{\phi}
Sacando factor común r:
                                                   z = r \left( \cos{\phi} + \mathrm{i}\sin{\phi} \right)
Frecuentemente, esta expresión se abrevia convenientemente de la siguiente manera:
                                                                \ z = r \; \operatorname{cis} \; {\phi}
Para definir un complejo según la ecuación se requieren dos parámetros, que pueden ser parte real e imaginaria o bien módulo y argumento, respectivamente.Según la Fórmula de Euler, vemos que:
                                              \cos{\phi} + \mathrm{i}\sin{\phi} = e^{\mathrm{i}\phi} ;\; z = r e^{i\phi}

- Potenciación ( Teorema de Moivre)

Sea Z = rcis 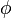\textstyle{\phi} , entonces

 Donde n pertenece a los naturales
- Radicación
Sea:



Lugares Geométricos
Distancia:





I Z I = 1   representa una circunferencia de centro (0,0) y radio = 1
Toda función se puede descomponer en parte Real e Imaginaria


Limite de una función compleja

Limites .- Sea f(z) una función compleja, de variable compleja, definida sobre un conjunto A y sea Z0 un punto de acumulación de A.

Se dice que el límite de la función f(z), cuando z tiende a z0, es L y lo escribimos:  

Si se verifica que:



Teorema:

Continuidad:

Exponenciales o Formula de Euler

Una variante de la forma polar se obtiene al tener en cuenta la conocida como formula de Euler

para .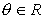


Funciones Hiperbólicas

senh(z) = (e^z - e^-z)/(2i)

cosh(z) = (e^z + e^-z)/(2)

propiedades
  • cos(iz) = cosh (z)
  • sen(iz) = isenh(z)

Derivadas de funciones de variable compleja







Una función de variable compleja se dice que f es derivable si y siempre y cuando el límite exista:



Las propiedades y reglas de derivación de las funciones de variable real se pueden aplicar para las funciones de variable compleja.



FUNCIONES TRASCENDENTES BÁSICAS 









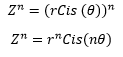
No hay comentarios:

Publicar un comentario

Suscribirse a: Entradas (Atom)